Main Research Topics
Quantum System Theory: Modeling, Stability, and Feedback Control
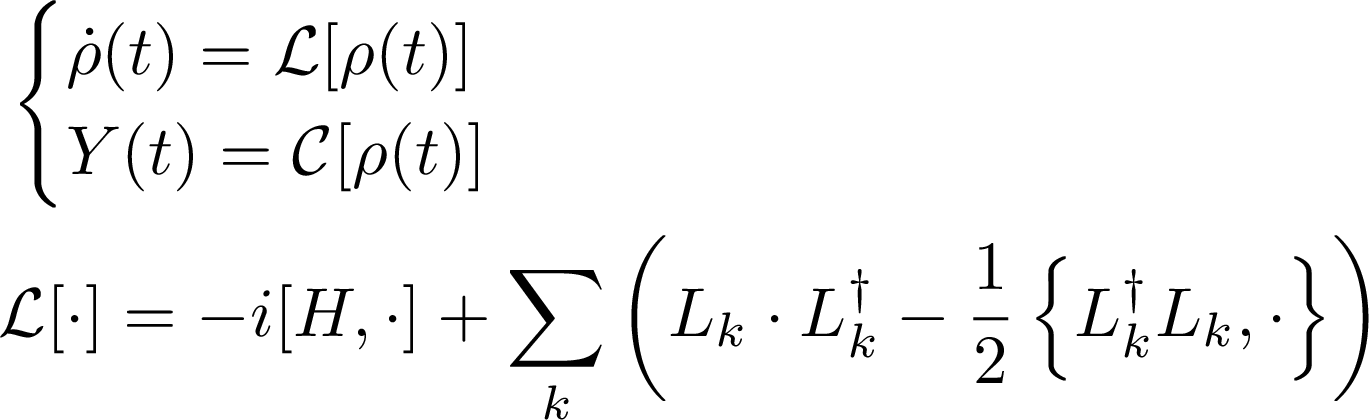
Since 2007, the group ongoing effort has been focused in developing system-theoretic methods for quantum systems, leveraging geometric ideas and Lyapunov methods.
In the past we characterized stable subsystems, assessed general methods for output feedback, studied the speed of convergence in quantum Markov dynamics, proposed hybrid open- and closed-loop stabilization approaches. Recently, we addressed the potential of switching (dissipative and not) dynamics for stabilization.
See the Publications page for related publications.
Model reduction, exact and approximate
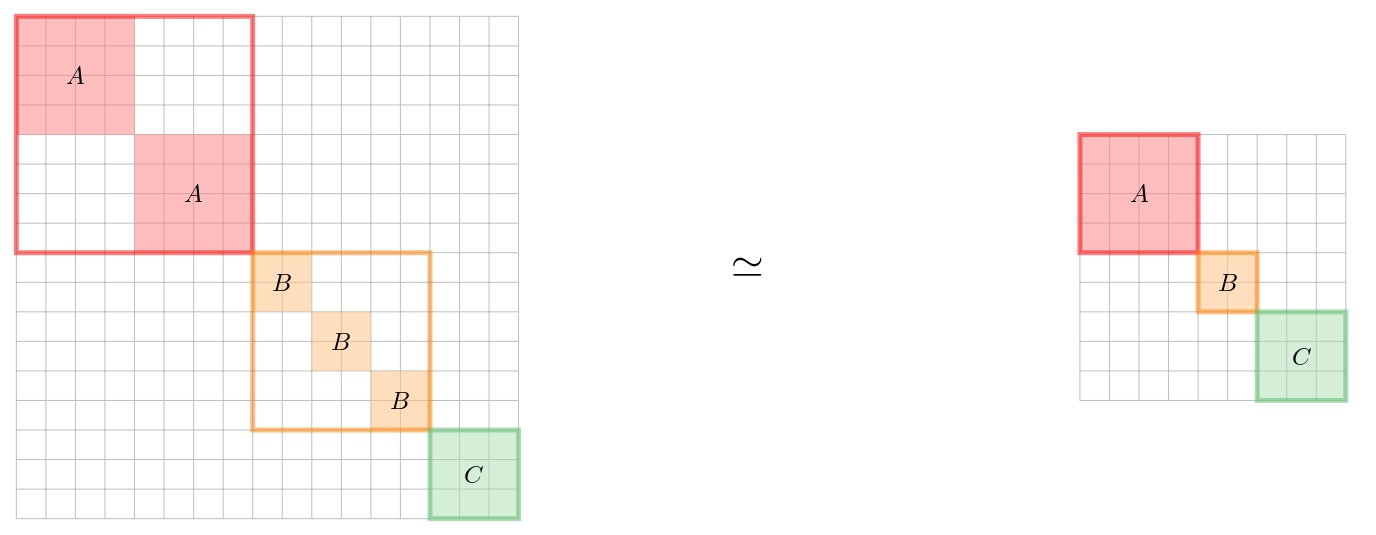
Finding simpler descriptions for dynamical models is a fundamental task in many scientific fields, including quantum physics. The main focus of this research area is to find reduced order models of quantum systems of interest while preserving the physical constraints given by quantum mechanics. When looking for reduced order models one could look for smaller description that reproduce the behavior of the original model exactly or smaller models that reproduce the behavior with a given accuracy. Both these directions are being investigated in our group.
The possible application of these model reduction techniques is manifold. Just to name a few: (1) finding better and more efficient ways of simulating quantum models on both classical and quantum computers; (2) obtain a better understanding of complex systems while focusing on simpler to study models; (3) constructing reduced-order state observers that allow for more efficient implementation of quantum controllers.
Furthermore this research area is tightly connected to relevant areas of interest for control system theory, such as hidden Markov models, positive systems, and complex networks.
Here is a short list of related papers we worked on:
Quantum noise control: Error correction and beyond
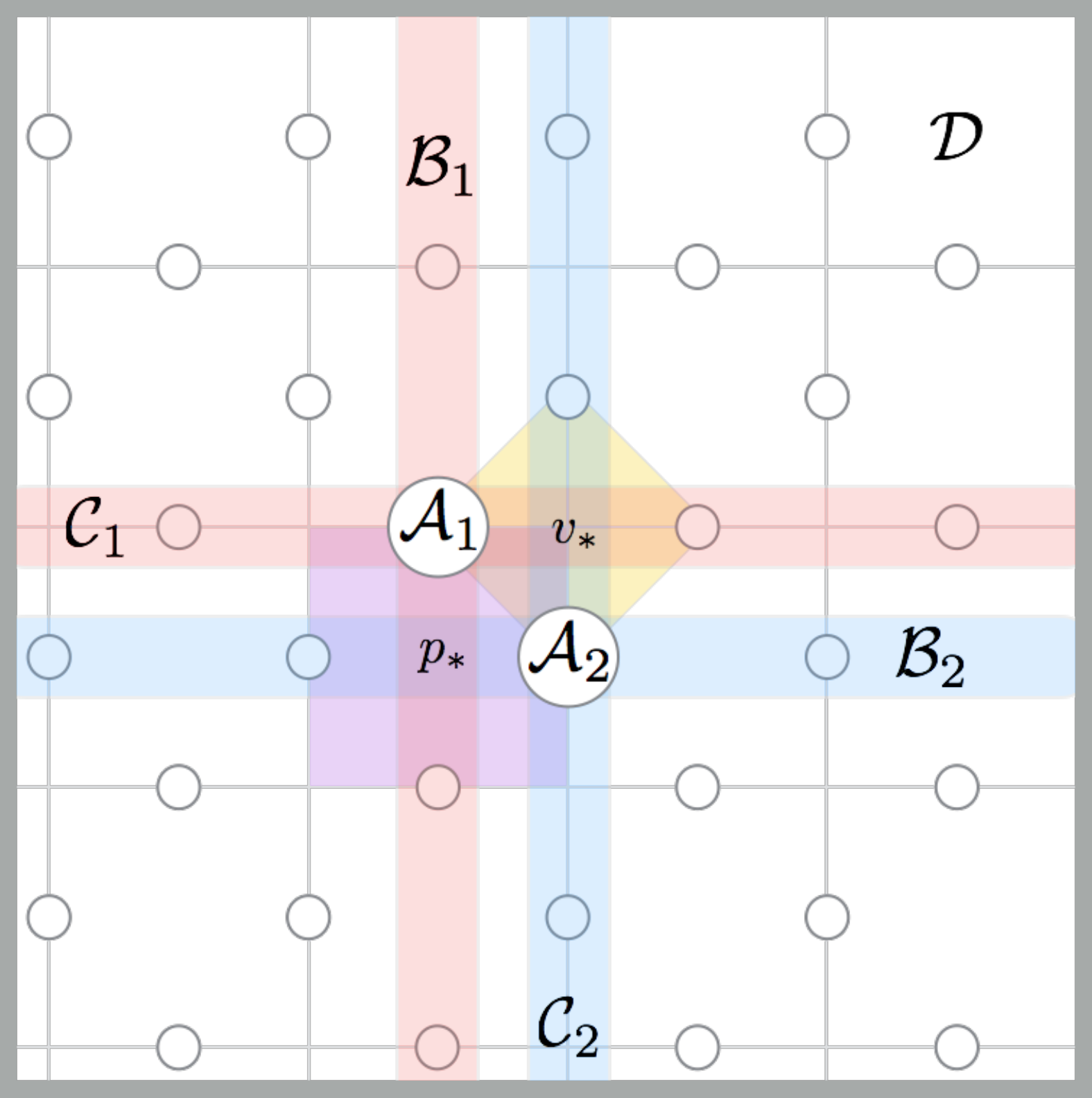
Quantum computation is still in the Noisy Intermediate-Scale Quantum (NISQ) era, due to the difficulties of fabricating and isolating scalable quantum devices. In order to overcome this era, different information protection methods are being designed, such as quantum error correction (QEC). The mitigation of noise and errors in quantum systems requires innovative solutions. In particular, the error-correcting techniques used in classical information processing are not applicable to quantum systems, mainly due to the quantum no-cloning theorem. Therefore, QEC is both of critical importance to the progress of the entire field and a challenging research area.
In a nutshell, QEC consists in (1) Embedding a logical quantum information into a larger physical system through an adequate encoding (2) Designing a recovery action that maps error affected states back into the correct encoded state. This process relies heavily on the knowledge of the dynamical properties of the system at hand and the noise that affects it. Subspace codes are the main type of encodings used in QEC, but it is known that finding correctable codes, even if the system dynamics is perfectly known, is an NP-Hard problem.
We are interested in systematic methods to (1) construct protectable codes and recovery maps for given noise models; (2) encode information in a given code in a robust fashion; (3) alternative approaches, using decoupling controls to isolate a target system for its environment.
Memory effects on classical and quantum network dynamics
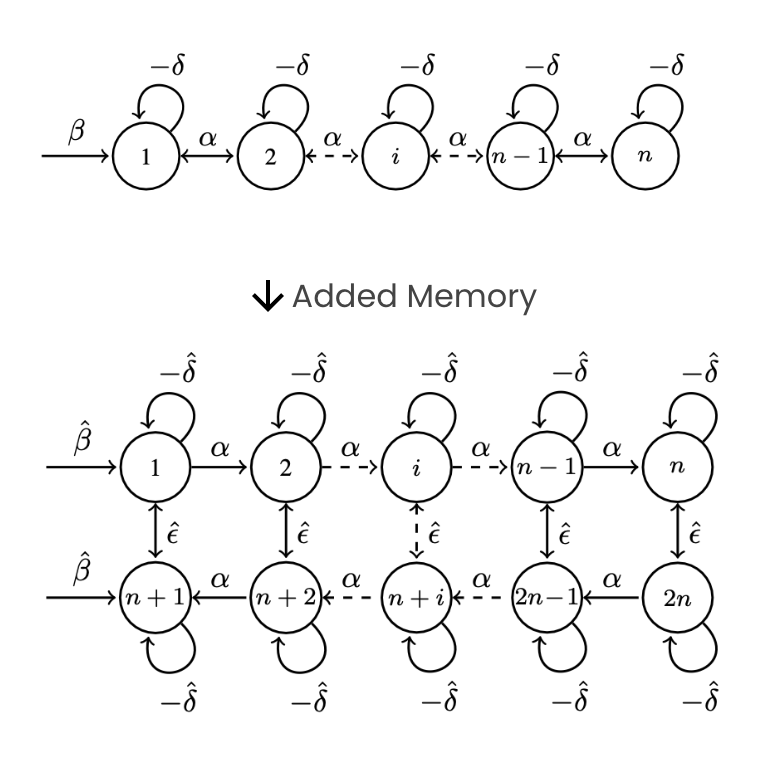
Over the past decade, control theory research has shifted its emphasis towards the modeling and control of increasingly interconnected networks, comprising possibly heterogeneous components. This shift in direction is primarily motivated by the number of compelling problems that can be described using networked dynamical systems. The research project lies at the boundary between classical and quantum network systems and control, with the aim to introduce new ideas, models and techniques to describe and optimize key dynamical properties of these systems.
The main focus of the project is in the description of memory-based effects, which are intrinsic in quantum systems over networks like quantum walks. It has been proven that these effects whether reproduced properly in classical systems may speed up the convergence of algorithms based on random walks.
We’re currently exploring how memory effects can be modeled in both classical and quantum systems: they can be translated into connectivity patterns within the network or a lifted version thereof. We’re illustrating how, by properly leveraging these effects, the control performance of the system under study can be enhanced
